Studienwochen
Das Departement Mathematik bietet jedes Jahr Anfang Juni eine Studienwoche für interessierte Gymnasiastinnen und Gymnasiasten an. In drei Gruppen werden in dieser Zeit unter Anleitung von Dozentinnen und Dozenten spannende Themen der Mathematik vorgestellt und erarbeitet. Gleichzeitig ist dies eine Gelegenheit, ETH-Luft zu schnuppern, etwa im Hinblick auf eine späteres Studium.
Die nächste Studienwoche findet Montag, 3. bis Freitag, 7. Juni 2024 statt.
Themenübersicht
Gerade hat in Zürich ein aufsehenerregendes neues Grand Hotel eröffnet. Das Besondere daran: Es hat unendlich viele Zimmer! Innerhalb kürzester Zeit haben sich unendlich viele Gäste aus aller Welt angemeldet, und alle Zimmer sind bereits belegt. Dennoch werden neue Besucher nicht abgewiesen, für jeden weiteren Gast kann ein Zimmer frei gemacht werden. Wie ist das möglich?
Mit diesen und ähnlichen Fragen über die Kuriositäten der Unendlichkeit wollen wir uns im Kurs beschäftigen. Wir werden zunächst den Begriff der Mächtigkeit von Mengen kennenlernen und sehen, dass zwei unendlich grosse Mengen nicht notwendigerweise gleich mächtig sein müssen, mehr noch, dass es sogar unendlich viele Abstufungen der Unendlichkeit gibt. Dies führt zu einigen überraschenden, teils paradox erscheinenden Ergebnissen. So kann man zum Beispiel zeigen, dass es "viel mehr" reelle Zahlen als rational Zahlen gibt.
Ausserdem wollen wir uns mit einigen klassischen Paradoxien beschäftigen. Unter anderem werden wir eine unendlich lange Trompete kennen lernen, die man mit endlich viel Farbe füllen, aber nicht mit endlich viel Farbe von aussen bemalen kann.

Es leuchtet ein, dass man ausgehend von Nichts auch nichts beweisen kann. Jede mathematische Theorie ist aufgebaut auf einem Fundament von Grundannahmen, einem sogenannten Axiomen System. Anhand des von Euklid (um 300 v.Chr.) eingeführten Axiomen Systems für die Geometrie studieren wir diesen Begriff ausführlich.
Nach Euklid haben Mathematiker:innen während Jahrhunderten vergeblich versucht zu zeigen, dass Euklid an einer gewissen Stelle (Stichwort Parallelenaxiom) ein Fehler unterlaufen ist. Noch anfangs des 19. Jahrhunderts beschwor ein durch seine diesbezüglichen, ebenso intensiven wie erfolglosen, Bemühungen völlig verzweifelter Mathematiker seinen Sohn in dramatischen Worten, sich auf gar keinen Fall auf diese Frage einzulassen. Aber der Sohn (J. Bolyai), wie das halt vorkommt, missachtete den väterlichen Rat. Wir vollziehen nach, wie er schliesslich, neben anderen Mathematikern (N. Lobatschewski, C.F. Gauss), in der zur Diskussion stehenden Frage zu völlig neuen, überraschenden Erkenntnissen kam, welche die Frage nicht nur abschliessend klärten, sondern dabei Tore zu völlig neuen mathematischen Welten öffneten.


Wie hat eigentlich Caesar mit seinen Freunden kommuniziert? Sicher hat er nicht einfach Briefe geschrieben, die man ohne weiteres lesen konnte. Dann wäre die Gefahr zu gross gewesen, dass Feinde seine Boten abgefangen hätten und so der Inhalt der Briefe bekannt geworden wäre. Daher hat Caesar seine Post verschlüsselt (allerdings nicht sehr gut, wie wir in diesem Kurs lernen werden). Seit den alten Römern hat sich viel getan, und die sichere Verschlüsselung von Nachrichten und Daten ist in unserer digitalisierten Welt immer wichtiger geworden. Wer will schon, dass alle unsere Selfies anschauen oder unseren Kontostand sehen können? Die heute üblichen Kryptoverfahren beruhen zum grossen Teil auf klassischen Ergebnissen der Zahlentheorie. Dieser Kurs behandelt einige klassische Verfahren, wie der Caesar- und der Vigenère-Chiffre, aber auch aktuell relevanten Kryptosysteme, wie das RSA-Verfahren. Dabei werden mathematische Grundlagen aus der Zahlentheorie verwendet. Ausserdem werden die untersuchten Kryptoverfahren am Computer implementiert, sowie verschiedene Angriffe diskutiert und durchgeführt.
Die Kreiszahl kommt als halber Umfang des Einheitskreis in vielen geometrischen Berechnungen auf ganz natürliche Weise innerhalb und ausserhalb der Mathematik vor. Doch warum tritt 𝜋 auch in der Zahlentheorie bei Betrachtung von natürlichen Zahlen häufig auf? Als Beispiel einer derartigen Aussage werden wir das Basler Problem
$$
\sum_{n=1}^{\infty}{\frac 1{n^{2}}}={\frac {\pi^{2}}{6}}
$$
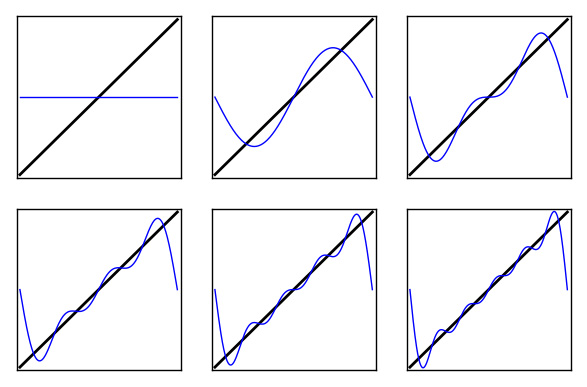
welches 1734 von Euler gelöst wurde, betrachten. Damit wir die Aussage und den Beweis verstehen können, werden wir uns auch mit Grenzwerten, Ableitungen und Integralen beschäftigen. Denn für den Beweis vom Basler Problem wollen wir Fourier-Reihen von gewissen Funktionen betrachten. (Eine Fourier-Reihe zerlegt ein periodisches Signal in Grundton und Obertöne, wie sie auch in der Musiktheorie vorkommen.) Kenntnisse über die Ableitung einfacher Funktionen werden wir kurz wiederholen, abgesehen davon wollen wir nur Interesse und Ausdauer voraussetzen.

Kurven begegnen uns tagtäglich. Wie muss man im Strassenbau eine Kurve konzipieren, um das Unfallrisiko zu minimieren? Auf welchen Bahnen bewegen sich Himmelskörper? Warum irrte sich Galileo Galilei, als er meinte, eine frei hängende Kette habe die Form einer Parabel? Und warum fällt das Wahrzeichen von Saint Louis nicht um? Auf welcher Rutschbahn rutscht man am schnellsten? (Es ist nicht die Gerade!) Wie lang darf eine Leiter maximal sein, damit man mit ihr in einem engen Korridor noch um die Ecke kommt? Wie funktionieren die Flüsterbögen in alten Gewölben? Dieses Thema entführt Sie auf eine Entdeckungsreise in die Welt der Kurven.

Wir wollen auf eine Reise durch die Welt der Zahlen gehen und dabei feststellen, dass es viel zu sehen gibt. Jeder weiss, dass es Quadratzahlen und Primzahlen gibt. Aber was haben diese miteinander oder mit Gauss- oder Hurwitz-Zahlen zu tun? Gibt es unendlich grosse Zahlen? Wozu ist die Wurzel aus -1 gut? Für den Computer ist 1 + 1 = 0, macht das Sinn und warum braucht man 'neue Zahlen' für Datensicherheit auf Festplatten? Auch wollen wir wissen: Was ist so speziell am Goldenen Schnitt, dass dieser in der Natur so oft vorkommt?
Wir wollen diese Fragen beantworten. Doch wie können wir uns der Antworten sicher sein, wenn wir ganz exotische neu gefundene Zahlen betrachten? Nur dann, wenn wir auch ein wirklich gutes Argument dafür, also einen Beweis für unsere Antwort, finden. Dabei wird unser einziges Axiom sein, dass Sie bereits die natürlichen und ganzen Zahlen kennen.
Zuletzt wollen wir noch fragen, was Zahlen mit Geometrie zu tun haben? Auch hier gibt es überraschende Antworten zu sehen.
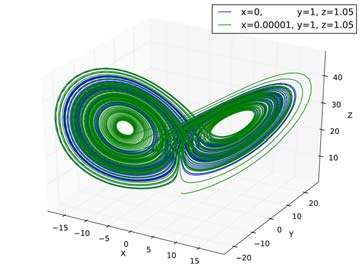
Leben bedeutet Veränderung. Ob es um die Position eines Fussballs, um die Anzahl Bakterien oder um den Wert des Blutdrucks geht, Veränderung macht das Leben interessant.
Die entsprechenden mathematischen Modelle sind Differentialgleichungen, die meistens nur numerisch, also mit dem Computer lösbar sind. Das heisst, es gibt keine geschlossene mathematische Formel für deren Lösung.
Wir lernen gewöhnliche Differentialgleichungen kennen, und wir bestimmen ihre Lösungen numerisch. Nebenbei machen wir uns spielend mit der Programmiersprache Python bekannt, die heutzutage eine wichtige Rolle spielt, z.B. bei der Entwicklung von Computerspielen, bei Google- und YouTube-Anwendungen oder bei wissenschaftlichen Simulationen und der Steuerung komplexer Luft- und Raumfahrt-Systeme.

We will investigate systematically and with mathematical rigor some of the fascinating properties of the integers 1, 2, 3, 4, ... and specifically, of the prime numbers 2, 3, 5, 7, 11, 13, 17, .... We will then discuss applications of the theory to cryptography, the study of how secret information (such as passwords or bank account details) can be communicated efficiently and securely.
Suppose Alice and Bob have never spoken privately before and now everyone can hear everything they say to each other. Can Bob nevertheless communicate a secret message to Alice? This seems to be impossible, but the surprising answer is yes! And prime numbers play a crucial role to make this miracle work.
The course starts completely from scratch and assumes no prerequisites.

Im Leben findet man viele Beispiele von grossen Netzwerken, in der Natur sowie im technischen Bereich. Beispiele sind das Internet, der globale Handel, Netzwerke von Pilzen im Waldboden oder die Zellen in unserem Gehirn. Graphentheorie ist die mathematische Sprache um diese Netzwerke zu beschreiben, und mit Wahrscheinlichkeitstheorie kann man Modelle von zufälligen Netzwerken bauen, die in der realen Welt statistischen Beobachtungen entsprechen. Im Laufe der Woche werden wir auf verschiedene Modelle von zufälligen Graphen eingehen und ihre Eigenschaften diskutieren. Zudem schauen wir uns an, inwiefern sie für die Modellierung konkreter Netzwerke aus der Natur und Technik relevant sind.
In diesem Zusammenhang wird es auch eine Einführung in die Graphentheorie, Wahrscheinlichkeitstheorie, statistische Modellierung und Computersimulation geben.

The INTEGERS - namely, the numbers 1,2,3,4,..., along with 0 and their negatives - are the first mathematical objects that we have ever encountered. We will be investigating some of the fascinating properties of these innocent-looking numbers.
An equation in two or more variables that is to be solved for INTEGER values of the unknowns is called "Diophantine". For example, can you write down some or even all triples of integers that are sides of a right triangle? One solution of infinitely many is 32 + 42 = 52. As we go along, the theory will be illustrated with various Diophantine equations. You will gain experience in writing formal rigorous mathematical proofs. The picture above shows a French stamp from 2001: Fermat's Last Theorem is the most famous Diophantine equation in the history of mathematics: There are no positive integers a, b, c and n > 2 such that an +bn =cn.



