
Richard Pink
Modular Cabinet

In Sprint 1996 I commissioned this cabinet from a professional carpenter. The design on the front is based on a mathematical pattern of straight lines and semi-circles, which is also shown separately below. From the mathematical point of view this pattern possesses many symmetries; most mathematicians will recognize it instantly. The Dutch artist Maurits Cornelis Escher produced impressive works on the basis of this and similar patterns. Some of its mathematical aspects can be understood without any special knowledge.
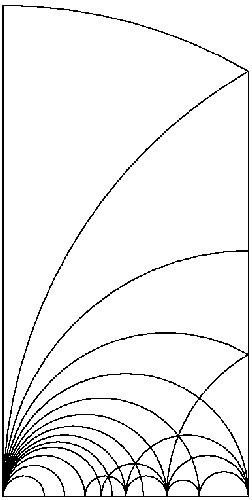
The cabinet is modular in two different meanings. On the one hand the mathematical pattern stems from the theory of so-called modular forms; its symmetry group is called the modular group. On the other hand the cabinet is modular in the technical sense: it can be taken apart and any smaller number of vertical elements can be assembled separately.
The pattern consists of vertical straight lines together with semi-circles all of whose centers lie on the lower horizontal axis. One should think of it as extended periodically to the whole upper half plane. Moreover, near the lower edge one should imagine infinitely many other semi-circles, becoming smaller and smaller, which for practical reasons cannot all be shown. One special aspect of this arrangement lies in the fact that the lines can meet only in certain regular ways. Namely, in the interior there are only two kinds of meeting points: either precisely two lines meet at an angle of 90 degrees, or precisely three lines meet at angles of 60 degrees each. At the lower edge there are always infinitely many semi-circles emanating from the same point. Furthermore, one should view all vertical lines as meeting in a hypothetical point at infinity.
If we cut the half plane along all these lines, each connected piece is a distorted triangle whose borders are straight and/or circular lines. Every triangle possesses precisely one angle of 90 degrees, one angle of 60 degrees, and one angle of 0 degrees. The angles of 0 degrees are those at the lower edge, where the lines meet each other tangentially. Thus in some sense all these triangles are similar. (The fact that the sum of the angles in such a triangle is different from 180 degrees is made possible by the fact that its borders need not be straight.) The analogous statements hold for the pieces which extend upwards to infinity, because we think of their borderlines as meeting at infinity, again in an angle of 0 degrees.

The most interesting property of this pattern is the fact that it remains completely unchanged under reflection at any of its lines. For the vertical straight lines this is obvious, which, incidentally, provided the idea to compose the cabinet from pairwise mirror symmetric vertical elements. The reflection at one of the semi-circles is not the usual one. Without defining it precisely one can visualize it as follows: The circle is turned inside out in such a way that the former interior covers all the exterior. The nearer a point was to the center of the circle, the farther away its mirror image will lie and the more a neighborhood of the point is being stretched. Conversely, the exterior of the circle is squeezed inside without creating plaids, and the farther away a region lies, the more it is being contracted. One useful property of this special kind of reflection is the fact that every circle or straight line is mapped to another circle or straight line. In particular, the whole pattern is mapped to itself. Even without much mathematical experience one can verify from the sketch below that the arrangement of different triangles to each other is invariant under these reflections.
In mathematical language this is a tesselation of the upper half plane
by fundamental domains for the action of the arithmetic group GL(2,Z).
Two neighboring glass doors together form the usual fundamental domain
for the group SL(2,Z). In complex coordinates the action is
easily described as follows: Two points z and w are equivalent if and
only if there exist integers a, b, c, d with ad-bc=+1 or =-1, such that
w or its complex conjugate is equal to (az+b)/(cz+d).
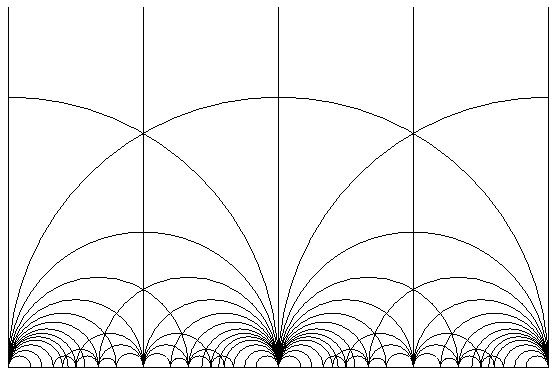
The upper half plane carries the structure of a so-called hyperbolic plane, that is, of a certain non-euclidean geometry. Here the distance of two points is redefined in a new way. Just as a straight line in euclidean geometry can be characterized as the shortest path between two points, in this geometry the shortest paths between two points, called geodesics, are precisely the vertical straight lines and the semi-circles whose centers lie on the horizontal axis. All lines in this pattern are such geodesics.
Design and Realization
My aim was to create an aesthetically pleasing object of everyday use with a deeper meaning in my own area of mathematics. After deciding on the basic ideas and some preliminary sketches on my part, the final concept was developed in collaboration with the master carpenter Urban Brenner, who eventually built the cabinet in his shop.

The decision to base the design of a cabinet on the above pattern came quite naturally, as this made it possible to realize at least some of the lines as the natural borderlines of doors. Each of the 8 vertical elements of the cabinet has a glass door above and a wooden door below. While each upper door represents a single hyperbolic triangle, the lower doors carry the rest of the pattern in the form of inlays. A circle segment as border between the two doors imposed itself as inevitable; this segment is continued as a black vein on the neighboring wooden doors. Inside the cabinet the curved borderline of the wooden door is taken up again by a similarly curved board. For practical reasons the boards above that are horizontal, as usual, although they thus do not correspond to anything in the original mathematical pattern. In order not to disturb the visual impact from this pattern any further, all other design elements were avoided, except the handles. For this reason the glass doors were constructed without a frame. This principle also helped to keep the costs within an acceptable range.
The curved borderline between the lower and upper doors alone significantly increased the technical difficulties in the production of the cabinet. Many individual steps (cutting, gluing of the veneer, gluing of the curved boards, etc.) had to be done by hand using a previously built mould. The work on the wooden doors with their fine inlay work required extreme care and precision. To have some reserve in the case of damage, the inlay sheet was ordered in 10 copies. This reserve turned out to be fully necessary!

The inlays themselves were made by a specialist with the help of a
computer controlled laser cutter, which achieved an almost unbelievable
precision. For each door one veneer sheet of particularly fine Canadian
maple and one of blackened wood of a different kind were cut by the
laser; the individual pieces were then reassembled by hand and glued.
The result of this excellent work, both by the specialist and by Urban
Brenner, can be admired in my house if you pay me a visit.
For
further Photographs click here
Contact
To my knowledge this cabinet is the only one of its kind in the world
so far. If you want a copy or a similar one made for yourself, I would
be glad to assist you. Please contact me or Urban Brenner in this
case. We do, however, retain the right to any commercial use of this
concept. If you know of furniture or other beautiful objects with a
mathematical background, or have any ideas for such things, I would be
glad to hear from you.
| Richard Pink | Schreinerei
Urban Brenner Siedlungsweg 7 D - 72202 Nagold Germany Tel.: +49-7452-4904 Fax: +49-7452-3865 |