Null- und Polstellen zählende Umlaufzahl
Mit diesem Applet demonstrieren wir den Satz von der Null- und Polstellen zählenden Umlaufzahl am Beispiel einer rationalen Funktion.
Das Applet arbeitet mit der rationalen Funktion $f: \mathbb{C} \to \mathbb{C}$ definiert durch $f(z) = \frac{z^2 + az + b}{z^2 + cz + d}$ für $a, b, c, d \in \mathbb{R}$. Sie können die Koeffizienten $a,b,c$ und $d$ verändern.
In der linken Ebene sind die Nullstellen (magenta) und Polstellen (schwarz) von $f$ eingezeichnet. Fahren Sie mit der Maus über die linke Ebene, wird ein Kreis mir Radius $2$ um den Mauszeiger gezeichnet. In der rechten Ebene sehen Sie sein Bild unter $f$.
Mit gedrückter Maustaste können Sie in der linken Ebene beliebige Wege einzeichnen.
Aufgaben und Fragen
Unter Umlaufzahl verstehen wir die Umlaufzahl des Bildweges im Bezug auf den Nullpunkt in der rechten Ebene.
- Verifizieren Sie den Satz von der Null- und Polstellen zählenden Umlaufzahl, indem Sie jeweils die Umlaufzahl bestimmen.
- Beobachten Sie, was mit dem Bild eines Kreises geschieht, wenn Sie ihn über eine Null- respektive Polstelle bewegen.
- Das Bild einer Schleife, die alle Null- und Polstellen umläuft hat Umlaufzahl
-
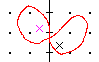 Das Bild der Schleife auf dem Bild hat die Umlaufzahl
Das Bild der Schleife auf dem Bild hat die Umlaufzahl
-
Untersuchen Sie die Fragen 1-4 für folgende Koeffizienten:
- $a=2,b=1,c=-1,d=2$
- $a=2,b=1,c=4,d=4$
- $a=1,b=5,c=2,d=1$
- Finden Sie Wege mit Umlaufzahlen gleich $0$, $\pm 1$ und $\pm 2$.